GSoC/2024/StatusReports/KenLo
Creating Pixel Perfect Tool for Krita
Currently Krita from KDE doesn’t have a Pixel Perfect option, the name for an algorithm that visually smoothes out pixel art curves. The idea here is that whenever the user ends up with a L-shape with this option, it would smartly remove corner pixels so that the overall curvature looks less blocky and more clean. By introducing this functionality, Krita users looking to utilize the pixel art functionalities alongside with Krita’s features can have an easier time controlling the precision and aesthetics of their pixel art creations.
Mentors: Emmett and Tiar
Links:
Links to Blogs and other writing
Find the rest here : https://kenlo.hashnode.dev/
Work report
Figuring things out :
How do we want the option to be officially implemented? In Libresprite it is just a checkbox on the top. It has been suggested that this option be put under the sharpness widget when creating a brush, alongside a check for 100% sharpness which is the pixel brush requirement.
Where and how exactly do we want to create this algorithm? There are a few files that I noted that deal with brush presets and files that deal with producing actual artwork on the canvas. We need to figure out exactly how brushes in general work and then figure out how exactly we want this algorithm to interact with the brushes.
Here's how Libresprite implements pixel-perfect:
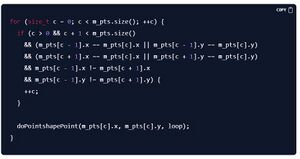
This loop iterates over all points in 'm_pts' and ignores certain points. There is a conditional check designed to skip over points that would visually form a corner in an L-like shape. While the current point is not the first or the last point in the vector, m_pts[c - 1].x == m_pts[c].x || m_pts[c - 1].y == m_pts[c].y checks if the previous point shares either the same x or y coordinate with the current point, and subsequently m_pts[c+1].x == m_pts[c].x || m_pts[c+1].y == m_pts[c].y checks if the next point shares either the same x or y coordinate with the current point. Then the rest of the code makes sure that the previous and next points do not share the x and y coordinates. Assuming all of the conditions are met c is incremented, basically skipping over the next point in the iteration. In practice, this code should detect a change in direction between the previous and next points (i.e, they do not lie on the same straight line but instead make a bend) and that the current point lies between two points that are aligned either vertically or horizontally but not diagonally.
Assuming Krita's drawing system isn't drastically different from how Aseprite's is implemented, we can assume a similar implementation where we track this list of points, along with pair adjacency and directions of points.
Obstacles:
The main problem I am running into right now is that for almost all function calls in the call hierarchy that draws, it isn't just clean input of all the pixel that is drawn, but instead a constant stream of these qPoint floats. In other words we are getting really frequent calls of these smaller points within the points (aka the floats) which makes everything harder to work with. This also explains why when drawing really slowly the lines get "blockier" or has more of thoose jagged extra pixels "doubles", mainly because we are getting really small line calls. This logic also explains why drawing faster results in cleaner lines that almost resembles pixel perfect lines, because we get bigger segments when calling drawDDALine.
Implementation :
After trying out a few different implementations (putting all the points in a vector and filtering out corners there, filtering out micropixels, changing what gets fed in drawDDALine), I ended up settling on a three point tracking system similar to that of the one from Tom Cantwell's blog . This implementation involves three important coordinates to track. 1.) The last drawn pixel, 2.) the “current pixel” - this is where your cursor currently is - and 3.) the “waiting pixel” which is an intermediary point that you have to keep track of, waiting to draw only until it’s confirmed to be in the desired direction. The idea is to wait to draw the next pixel (the waiting pixel that is always adjacent to the last drawn pixel) until we confirm that the current pixel is going in the same direction as the last drawn pixel. So while the current pixel is still adjacent to the last drawn pixel ( this is a straight line) the waiting pixel becomes the current pixel. While the current pixel is in the same direction as the last drawn pixel but further than one pixel away fill in the waiting pixel ( so that we can get a straight line ). Then for the case where the current pixel deviates and is no longer adjacent/in the same direction, we do not place the waiting pixel and instead change the last-drawn pixel to the current pixel.
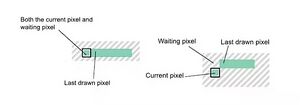
Adding on to this, I added a check for the axis, if the currentpixel is in the same axis as the lastdrawnpixel, we can draw waiting pixel and otherwise we skip it by just updating the waiting pixel to currentpixel without drawing. Also we want to make sure theres actually more than two pixels first before we look for a corner in the check above. This gets reset every time we skip a corner pixel because we would back to zero pixel in process again.

Conclusion:
So now that we are near the end, this is the results I have shown by my mentor Emmett. There are still a few edge cases where corners do show up and there are some jaggedness to some lines, but most of the time, it will be useful. I learned a lot, mostly about researching and learning a codebase for this project and I plan to finish up this project to make this feature fully bugless after GSOC.
